Highest Likelihood Decoding

5/21/2024

Code available here. Special thanks to help from Amanda Li and discussion with Jacob Springer and Vaishnavh Nagarajan.

Introduction

A causal language model takes in a sequence of tokens and produces a probability distribution over the next token, which is then sampled with some temperature. Lowering this temperature approaches greedily selecting the next token with the highest probability (illustrated in Figure 1). However, greedy decoding does not necessarily sample the sequence of tokens the model assigns the highest likelihood. This may be important for difficult tasks where quality is of the utmost importance. On the other hand, the highest likelihood generations may be unnatural/pathological. This motivates the following question: Is the highest likelihood string better than the greedy string?

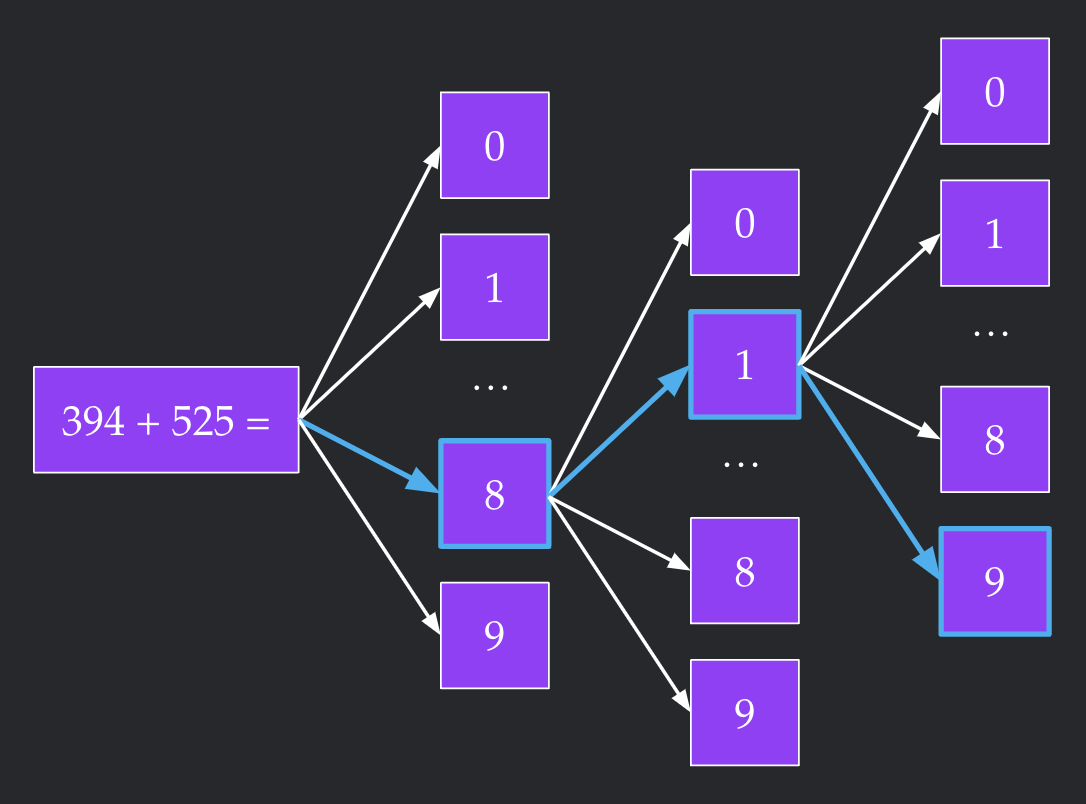
Figure 1: Example of greedy decoding for an arithmetic prompt. At each step, we use the model to select the next token instead of exploring the entire space of strings.

Highest Likelihood Decoding Algorithm

We would like to find the $k$ token sequence from a vocab size $V$ that achieves the highest likelihood under the model. The computational prohibitive brute force would be to try all $V^k$ possible completions. To get around this, we implement a depth-first search with two heuristics that significantly lower the runtime.

Our first heuristic is maintaining the best full-length sequence found so far. We note that the likelihood of a string can only decrease if you add more characters to it. Suppose we encounter an intermediate node of the tree, representing an uncompleted sequence of $< k$ tokens, which already has lower likelihood than our current best length $k$ sequence. Since the likelihood can only go down, none of the children are candidates for the highest likelihood sequence. Therefore, we can stop traversing down this node's children and move on to exploring other nodes.

Our second heuristic is re-ordering the children of any intermediate node by the likelihood of each child. Without the first heuristic, this re-ordering does not change the runtime of the algorithm at all. However, this heuristic will probably help us run into the highest likelihood sequence earlier. This complements the first heuristic quite nicely--since we run into better sequences earlier, we can prune more aggressively.

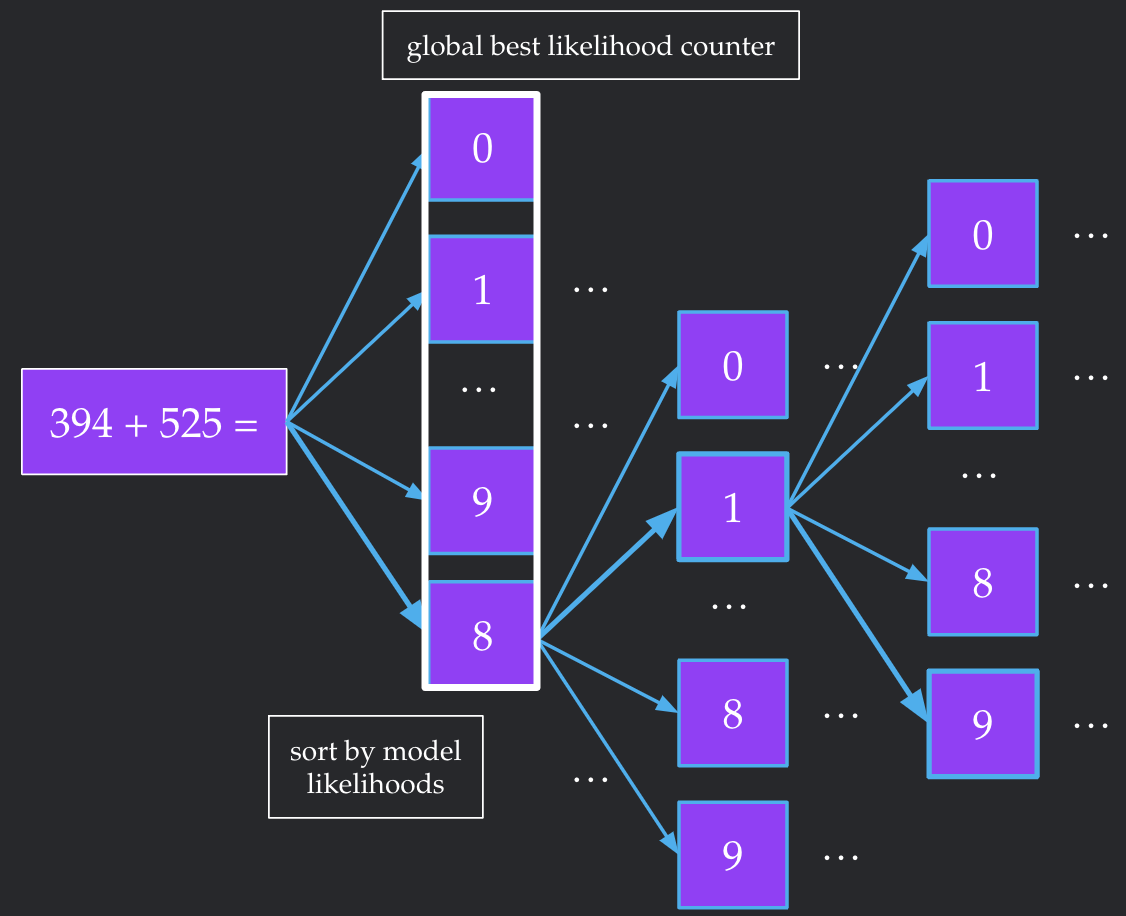
Figure 2: Highest likelihood decoding. We maintain a best likelihood counter for pruning during our DFS, while greedily re-ordering children to improve this counter.

Results

Due to computational limitations, we test with the relatively smaller open-source models of Pythia-70m, Pythia-160m, and Pythia-410m (Biderman et al, 2023). We test decoding from the model starting with the empty sequence (only the BOS token). To constrain the search space, we only use a 188 token subset sourced from common English words and sentences. We track the best completion for these models from lengths 1 to 8 in Table 1.

Table 1: Highest likelihood and greedy completions for lengths 1 to 8 from Pythia models.
	Pythia-70m	Pythia-160m	Pythia-410m
1	The	The	The
2	It is	We are	It is
3	I have a	It is a	I have a
4	We are in the	We are in the	We are in the
5	It is to me that	I I I I I	Look at me, I
6	The, and the, and	I I I I I I
7	The, the, the, the	I I I I I I I
8	I, I, I, I	I I I I I I I I
Greedy	The two in the two in the two	The two are the two that are the	The two are the two that have the

Interestingly, we find that the maximum likelihood completions appear coherent for shorter lengths while they degenerate for longer lengths. This indicates that highest likelihood decoding may have problems at longer sequence lengths, similar to how greedy decoding can lead to degeneration in other settings (Holtzman et al, 2019).

Our algorithm significantly speeds up finding the highest likelihood sequence. Specifically, for Pythia-70m length 8, the brute force algorithm would take 8344900976819085 forward passes while our algorithm only took 4792 forward passes. You can find more such logs in this folder.

Future Work

To me, the most exciting extension of this work is testing more difficult tasks that involve multiple steps or reasoning. One task I am particularly excited about is arithmetic, where one sees if the highest likelihood decoding does better than the greedy generation for addition problems. There are also several engineering considerations to make highest likelihood decoding faster such as cleverly managing the KV cache during search. Maybe I'll get around to these on a later date, maybe you can do it for me :P

Thank you for reading, and feel free to reach out with any questions or thoughts!