Understanding Reinforcement Learning from Human Feedback
9/6/2023
Language models are generally pre-trained on a corpus of internet text to learn how to model natural language and "the world". At scale, these models tend to fit text from the internet surprisingly well (Brown et al, 2020). However, this serves as a double-edged sword when it comes to utility, especially if we don't want the model to pick up the gigabytes of toxicity it processes. The most common approach to having models adapt to human requirements such as helpfulness and harmlessness (Bai et al, 2022) is fine-tuning via Reinforcement Learning from Human Feedback (RLHF). In this post, we'll sketch the broad strokes of the training procedure. Along the way, we'll develop an understanding of what's easy and hard in RLHF as well as discuss some open questions (with respect to the time this post was written).
Overview
In our discussion today, a language model is a function \(\pi\) which fits \(\mathbb{P}(x_{i+1} \mid x_1, x_2, \ldots x_i)\) (given \(i\) text tokens, consider what's likely or unlikely to follow). With this model, we can estimate the likelihood of a piece of text \(\mathbb{P}(x)\) through the chain rule and we can sample text conditioned on a prompt of interest.
We'll typically assume that we're doing a good job of pre-training on billions of tokens and we can estimate the "true" conditional probability for text drawn from the distribution of the internet. As discussed earlier, though this is really useful, it might not be what we want users to interact with. The following two-step recipe is generally followed to "RLHF" an initial model \(\pi_0\) into a more harmless and helpful model \(\pi\).
- Derive a reward model \(r\) such that \(r(x)\) measures how "desirable" string \(x\) is.
- Derive a \(\pi\) that maximizes reward while utilizing the "knowledge" in \(\pi_0\).
This simple algorithm is followed by some of the largest examples of RLHF such as OpenAI's InstructGPT (Ouyang et al, 2022) and Meta's LLaMa-2 (Touvron et al, 2023). We'll go into a bit more detail for each step. This will touch on the core aspects of RLHF at the cost of over-simplifying the actual training procedure.
1. Training a reward model
Finding a good reward model \(r\) is typically formulated as a learning problem. Human labellers assess model outputs as "desirable" or "undesirable" so that the reward model can learn these notions. Unfortunately, if we just asked humans to rank the text from 1 to 7, the label distribution might be different conditioned on different humans, even if they all agree which text is better or worse. To address this issue, model outputs are typically compared against each other, and humans specify which output is preferred.
Concretely, say that we wanted to learn a reward model \(r_{\phi}\) parameterized by \(\phi\). For prompt \(x\) picked from a curated dataset \(\mathcal{D}_R\), we sample two model completions \(y_1, y_2 \sim \pi_0(x)\). Then, based on what the human raters prefer, we identify one as the correct completion \(y_c\) and the other as the wrong completition \(y_w\). Since we know that \(r_{\phi}(x \texttt{ concat } y_c)\) should be higher than \(r_{\phi}(x \texttt{ concat } y_w)\), we can now minimize the following loss
\[\mathcal{L}_R(r_{\phi}, \mathcal{D}_R) = -\mathbb{E}_{(x, y_c, y_w) \sim \mathcal{D}_R} \left[ \log\left(\sigma\left(r_{\phi}(x \texttt{ concat } y_c) - r_{\phi}(x \texttt{ concat } y_w)\right)\right)\right]\]
where \(\sigma\) is the sigmoid function. This incentivizes the reward model to learn a function which can distinguish between good and bad samples. \(r_{\phi}\) is usually initialized with \(\pi_0\), though it's not agreed upon whether this is necessary for more subtle reasons than speeding up training. There are also simple modifications to this objective which can incorporate how much better \(y_c\) is compared to \(y_w\).
Training a good reward model is super hard! If your dataset is not big enough, it's easy to overfit the samples in your dataset and not generalize to unseen instances. Since this requires labelled data unlike unsupervised pre-training, it's incredibly expensive. For example, this blog post estimates that Meta spent $25 million to simply collect the preference data for their reward models!
2. Reflecting the rewards
Once we have this reward model \(r\), how do we get a new \(\pi\) to reflect these preferences? Well, we just formulate another learning problem :)) Suppose we had a dataset \(\mathcal{D}\) which represents text where we want the model to reflect the preferences captured by the reward model (this can be fully curated, completions sampled from curated prefixes, or purely sampled from \(\pi_0\)). In this case, our first attempt at deriving a \(\pi_{\theta}\) parameterized by \(\theta\) can be initializing at \(\pi_0\) and solving
\[\max_{\theta} \mathbb{E}_{x\sim\mathcal{D}, y \sim \pi_{\theta}}\left[r(x \texttt{^} y)\right]\]
However, naively optimizing this objective has some unintended consequences. The biggest problem is mode collapse, in that for any string, the model will never be encouraged to model a probability distribution but will rather output the piece of text that simply maximizes the reward. Since we would like to keep the effects of modelling a distribution, such as calibrated uncertainty in answering, we consider a slightly modified form of this objective as
\[\max_{\theta} \mathbb{E}_{x\sim\mathcal{D}, y \sim \pi_{\theta}}\left[r(x \texttt{^} y)\right] - \beta D_{KL}(\pi_{\theta}, \pi_0)\]
where \(D_{KL}\) is the KL divergence, or how far the first distribution is from the second. Therefore, this objective tries to maximize the reward function while staying close to the original distribution. This algorithm is often referred to as Proximal Policy Optimization, or PPO (Schulman et al, 2017).
Alternate view
We will briefly touch an alternative view of reflecting the rewards discussed by Korbak et al, 2022. For this, let's assume that our reward model can be normalized to capture the log-likelihood of a sentence \(x\) being "SATisfactory", or \(r(x) = \log \mathbb{P}(\text{SAT} | x)\). Depending on how strongly we want to reflect the reward model, we can scale it by a factor \(\beta\) and re-normalize to get \(\log \mathbb{P}(\text{SAT} | x) = \frac{r(x)}{\beta}\). If \(\beta\) is large, all text looks equally satisfactory, and the inverse is also true. Under this framework, our goal is to find the optimal model \(\pi^*\) that generates text conditioned on being satisfactory, which corresponds to \(\log \mathbb{P}(x | \text{SAT})\). Now, we can try to write this our explicitly as
\[\log \pi^*(x) = \log \mathbb{P}(x | \text{SAT}) = \log\left(\frac{\mathbb{P}(\text{SAT} | x)\mathbb{P}(x)}{\mathbb{P}(\text{SAT})}\right) = \frac{r(x)}{\beta} + \log \pi_0(x) - C\]
Under this, we observe that RLHF is simply interpolating between the original model and the preferences expressed by the reward model!
Conclusion
Now that we're intimate with the actual training algorithm, we can discuss what exactly is going on. During the first step of reward modelling, the objective is to learn the human preferences that we want to reflect this, which is communicated through the human labellers. From there, the actual fine-tuning is simply distilling this information into the model. In fact, Rafailov et al, 2023 show that both these stages can be merged into direct updates from the preferences dataset.
My understanding is that the true difficulty lies in the first step of specifying the rewards. In general, specifying desired properties is incredibly difficult. As discussed earlier, it is incredibly expensive to collect supervised data and preference datasets are nowhere near as expansive as unsupervised pre-training datasets. Moreover, the second step may introduce some additional problems if our reward model or loss regularization doesn't explicitly capture what properties we want to preserve. For example, RLHF can destroy the calibration of models, as shown in Figure 1 (OpenAI, 2023). Since we don't have a strong method of specifying we want calibration, its unclear whether the current method is capable of preserving this property. More broadly, there is likely important work in understanding how to optimize the model to reflect nuanced specifications that go beyond univariate human rewards.
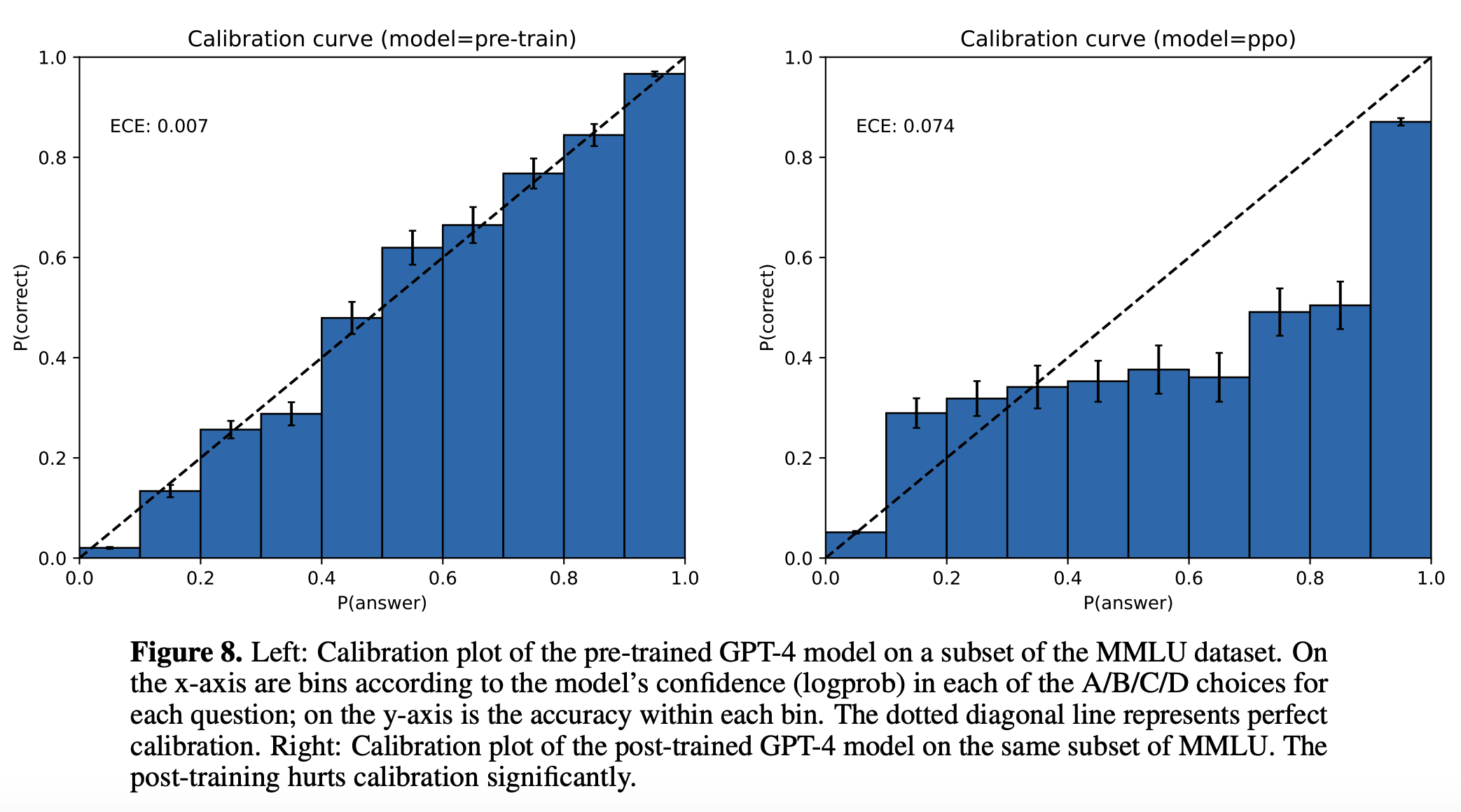
Figure 1: Page 12 of OpenAI, 2023
After writing this post, I came across Casper et al, 2023, which provides an incredibly comprehensive analysis of tractable and fundamental problems with RLHF based on the pipeline I discuss above. I highly reccomend checking out this resource if you are interested in the full taxonomy of current problems, rather than a few problems of personal interest. I hope this post elucidated the strengths and weaknesses of RLHF! Thanks for reading, and please reach out with any questions or comments!